
什么是皮尔逊相关系数(Pearson Correlation Coefficient)?
相关系数(Pearson product moment correlation coefficient)是用 -1 到 1 之间的数值来表示两个变量相关程度的指标。当正相关越强时,相关系数趋近于 1;而负相关越强时,相关系数则趋近于 -1。
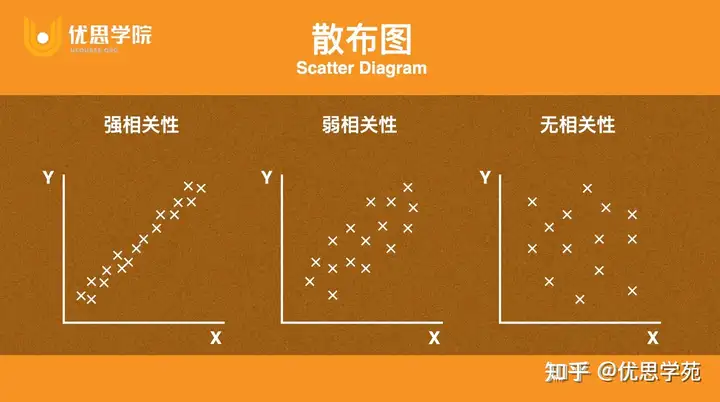
通过观察两个变量的离差乘积,我们可以发现:当两个变量都比各自的平均数大或小时,相关系数为正数。这是因为在正相关较强的情况下,符合此条件的数据较多,使得离差乘积的总和为正数。
反之,当其中一个变量大于平均数而另一个小于平均数时,两个变量的离差乘积为负数。在负相关较强的情况下,由于此类数据较多,离差乘积的总和即为负数。
数学含义
为了消除数据量对结果的影响,我们通过将离差乘积的总和除以数据量来计算平均值,这个平均值称为共变数(S)。然而,共变数仍可能受到使用不同测量单位的数据的影响,因此,我们通过将共变数除以各个变量的标准差的乘积来调整,得到的结果即为相关系数(r)。
公式如下:
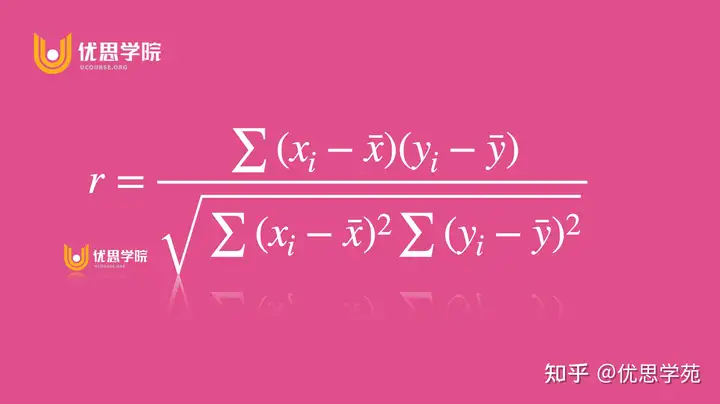
这里,Xi 和 Yi 分别是两个变量的观察值,Xˉ 和 Yˉ 是它们的平均值。分子部分是协方差,它衡量了两个变量的变动趋势是否一致。分母是两个变量标准差的乘积,用来标准化结果。
本质
皮尔逊相关系数的本质是通过标准化的协方差来评估两个变量之间线性关系的强度和方向。这意味着它可以告诉我们,在一个变量增加的时候,另一个变量是增加还是减少,以及这种变化的一致性有多强。
使用场景
- 正相关:当一个变量增加时,另一个变量也增加,相关系数接近+1。
- 负相关:当一个变量增加时,另一个变量减少,相关系数接近-1。
- 无相关:两个变量之间没有明显的线性关系,相关系数接近0。
皮尔逊相关系数广泛用于统计分析中,特别是在需要评估两个量化数据间关系的强度时。它对数据的分布做出了正态分布的假设,因此在数据显著偏离正态分布时使用它可能不太合适。此外,它也不能很好地处理离群值或非线性关系。
六西格玛中的应用
在六西格玛(Six Sigma)项目中,相关系数 r 是一个重要的统计工具,用于衡量两个变量之间的线性关系强度和方向。通过了解变量之间的相关性,六西格玛项目能够识别关键输入变量(KPIVs)和关键输出变量(KPOVs)之间的关系,从而帮助项目团队确定哪些因素对过程性能有显著影响。











是什么?-80x80.webp)









